Logo

菜单

Administrator
Administrator
发布于 2025-10-17 / 20 阅读
0
0

c语言ASCII旋转甜甜圈

原创Donut math: how donut.c works

这是个让我很感兴趣的项目,整体大概是这个样子.


             k;double sin()
         ,cos();main(){float A=
       0,B=0,i,j,z[1760];char b[
     1760];printf("\x1b[2J");for(;;
  ){memset(b,32,1760);memset(z,0,7040)
  ;for(j=0;6.28>j;j+=0.07)for(i=0;6.28
 >i;i+=0.02){float c=sin(i),d=cos(j),e=
 sin(A),f=sin(j),g=cos(A),h=d+2,D=1/(c*
 h*e+f*g+5),l=cos      (i),m=cos(B),n=s\
in(B),t=c*h*g-f*        e;int x=40+30*D*
(l*h*m-t*n),y=            12+15*D*(l*h*n
+t*m),o=x+80*y,          N=8*((f*e-c*d*g
 )*m-c*d*e-f*g-l        *d*n);if(22>y&&
 y>0&&x>0&&80>x&&D>z[o]){z[o]=D;;;b[o]=
 ".,-~:;=!*#$@"[N>0?N:0];}}/*#****!!-*/
  printf("\x1b[H");for(k=0;1761>k;k++)
   putchar(k%80?b[k]:10);A+=0.04;B+=
     0.02;}}/*****####*******!!=;:~
       ~::==!!!**********!!!==::-
         .,~~;;;========;;;:~-.
             ..,--------,*/

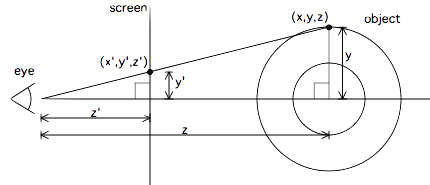
这涉及到圆以及旋转矩阵还有投影

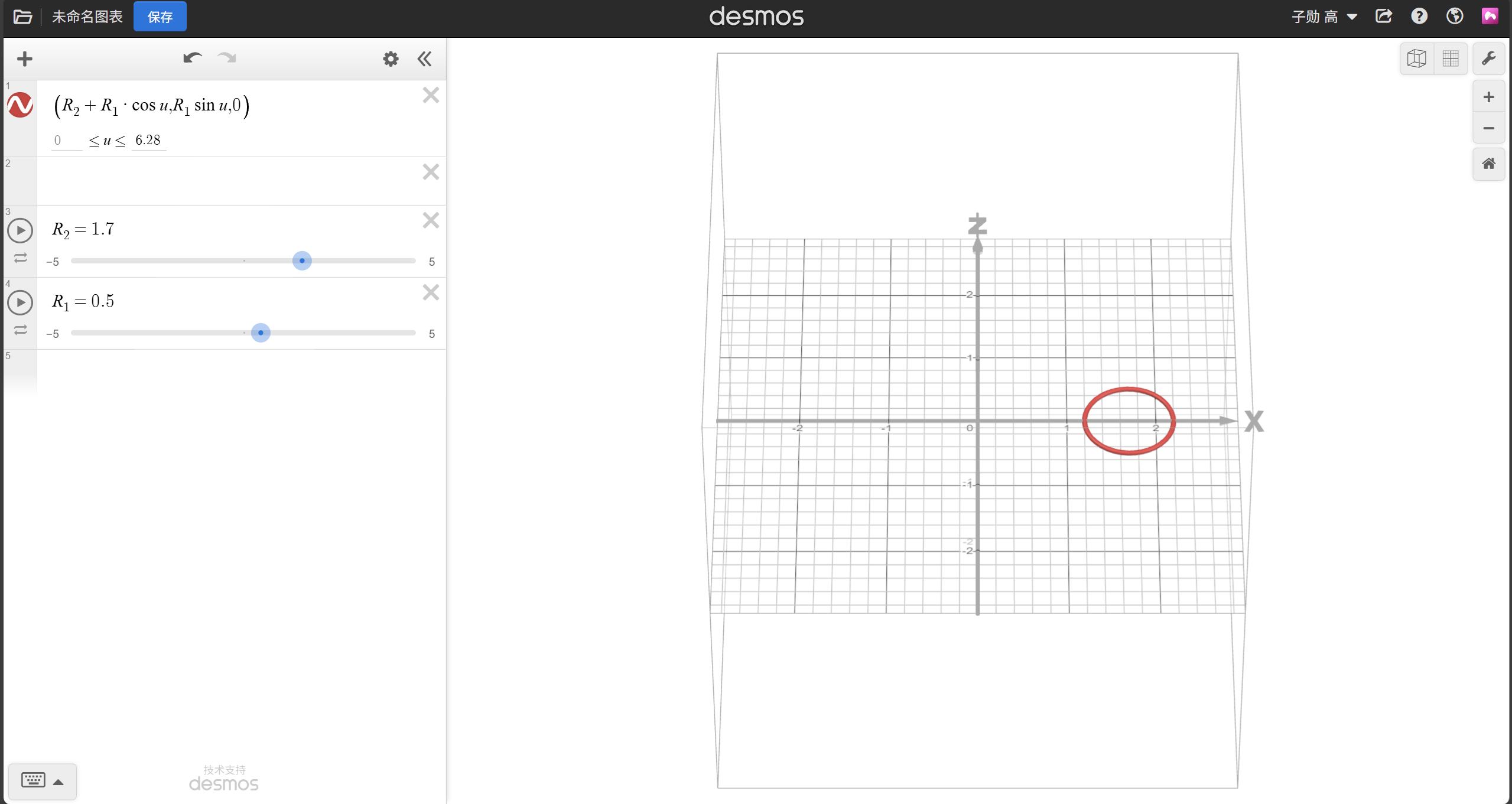
R1控制圆的大小，R2控制圆距离原点的距离。

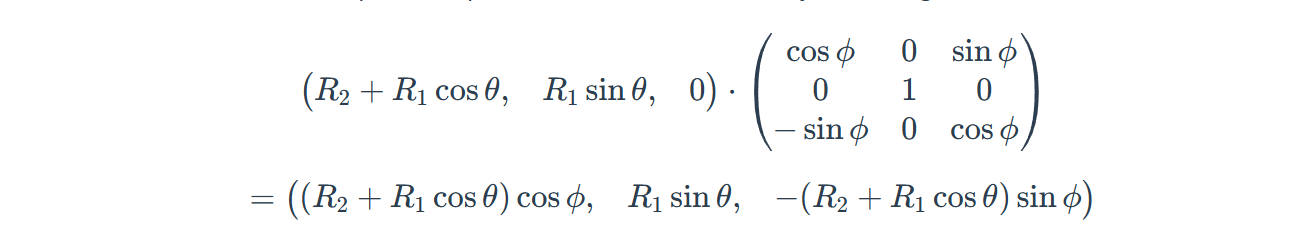
接下来乘以旋转矩阵得到绕y轴旋转的方程得到如下图形。

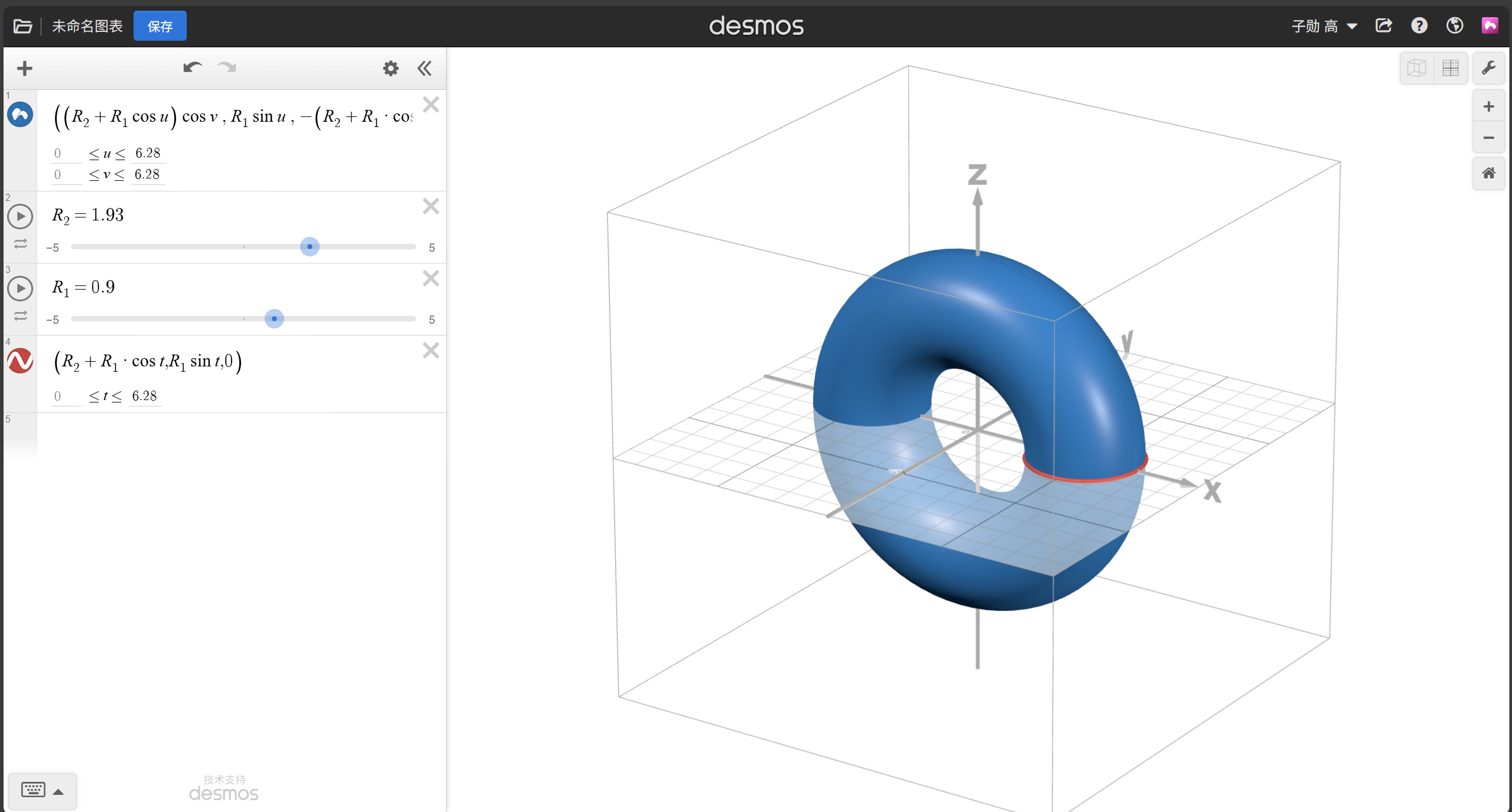
如果乘以三个方向的旋转矩阵就会旋转

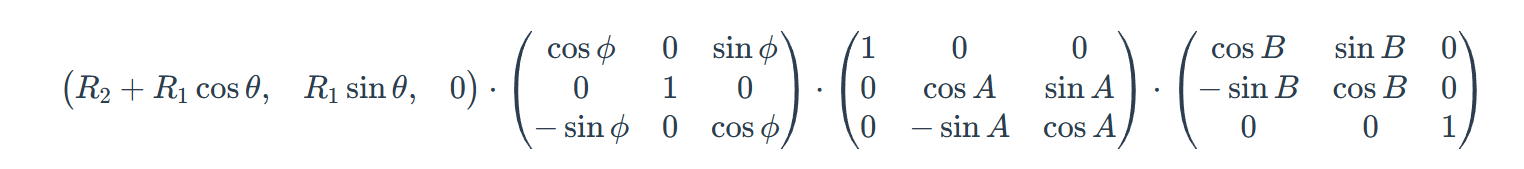
现在需要将三维的转化到二维屏幕上

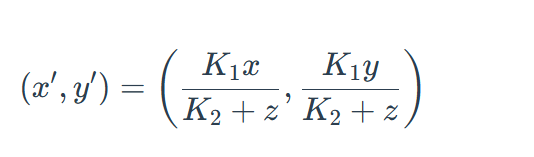
通过定义K2改变图形投影在屏幕上的大小

所以最终的计算方程应该是

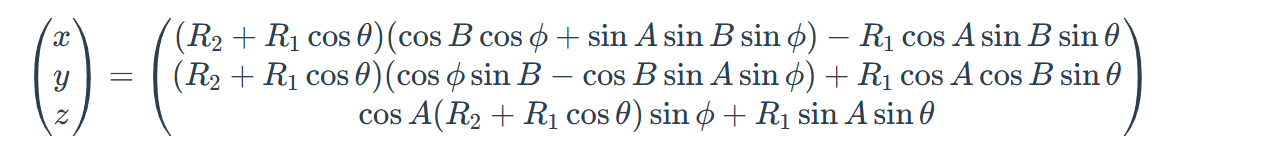
但是文章中提到的还有关于光照的计算通过改变字符来实现明暗变化

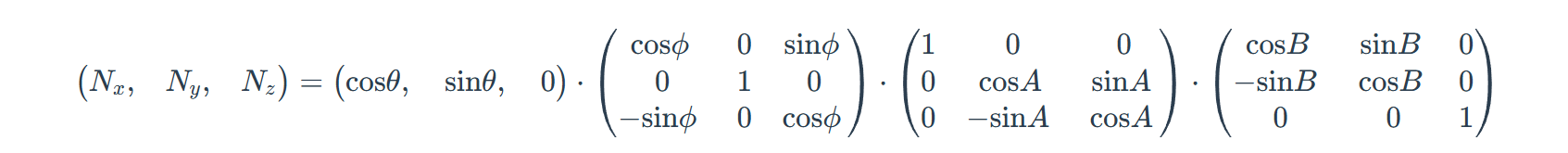
也就是如上计算公式

最终代码如下

#include <stdio.h>
#include <math.h>
#include <unistd.h>

const float ta_s = 0.07f;
const float phi_s = 0.02f;
const float pi = 3.1415926535f;

const float R1=1;
const float R2=2;
const float K2=5;
const int s_w = 20;
const int s_h = 20;
float A,B = 0;


const float K1 = ((float)s_w * 3 * K2) / (8 * (R1 + R2));


int main() {


    for (;;) {
        float cosA = cosf(A), sinA = sinf(A);
        float cosB = cosf(B), sinB = sinf(B);

        char output[s_w][s_h];
        float zbuffer[s_w][s_h];

        for (int y = 0; y < s_h; y++) {
            for (int x = 0; x < s_w; x++) {
                output[y][x] = ' ';
                zbuffer[y][x] = 0.0f;
            }
        }


        for (float ta=0; ta < 2*pi ; ta += ta_s) {
            float costa = cosf(ta), sinta = sinf(ta);

            for (float phi=0; phi<2*pi; phi+=phi_s) {
                float cosphi = cosf(phi) , sinphi = sinf(phi);
                float cx = R2 + R1*costa;
                float cy = R1*sinta;


                float x = cx * (cosB * cosphi + sinA * sinB * sinphi) - cy * cosA * sinB;
                float y = cx * (sinB * cosphi - sinA * cosB * sinphi) + cy * cosA * cosB;
                float z = K2 + cosA * cx * sinphi + cy * sinA;
                float ooz = 1.0f / z;

                int xp = (int)((s_w / 2) + K1 * ooz * x);
                int yp = (int)((s_h / 2) - K1 * ooz * y);

                float L = cosphi * costa * sinB - cosA * costa * sinphi -
                         sinA * sinta + cosB * (cosA * sinta - costa * sinA * sinphi);

                if (xp >= 0 && xp < s_w && yp >= 0 && yp < s_h) {
                    if (L > 0 && ooz > zbuffer[xp][yp]) {
                        zbuffer[xp][yp] = ooz;
                        // 确保亮度索引在有效范围内
                        int luminance_index = (int)(L * 8);
                        if (luminance_index < 0) luminance_index = 0;
                        if (luminance_index >= 12) luminance_index = 11;
                        output[xp][yp] = ".,-~:;=!*#$@"[luminance_index];
                    }
                }

            }


        }
        printf("\r\x1b[23A");
        for (int j = 0; j < s_h; j++) {
            for (int i = 0; i < s_w; i++) {
                putchar(output[i][j]);
                A+=0.00005;
                B+=0.00002;
            }
            putchar('\n');
        }
        usleep(15000);
    }
}

评论